
TG-WEBの計数では三段論法を使わないと解けない問題が出題されることがあります。
※「TG-WEBとは?対策法や例題を完全解説!TG-WEBはこれで完璧だ」もぜひ合わせてご覧ください。
三段論法という言葉を聞いたことがある人は多いでしょうが、具体的に三段論法がどんなものかわかっていない人も多いのではないでしょうか?
本記事ではTG-WEBを今までに100回以上も受検し、日本で一番TG-WEBに詳しい自信のある私タケルが、三段論法とは何かについて解説した後、TG-WEBで出題される三段論法が必要な問題もご紹介していきます。
TG-WEBを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、TG-WEBにはたった3時間の勉強でTG-WEBが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものTG-WEB受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
TG-WEBの三段論法とは?
冒頭でも解説した通り、TG-WEBの計数では三段論法を使用した問題が出題範囲に含まれています。
TG-WEBには従来型と新型の2種類がありますが、三段論法を使用した問題が出題されるのは従来型のみです。
※従来型は旧型とも呼ばれています。従来型の詳細については「TG-WEB従来型とは?例題・試験時間・問題数もすべて解説!」をご覧ください。
三段論法とは「AならばB」と「BならばC」が成り立つとき、「AならばC」が成り立つことです。
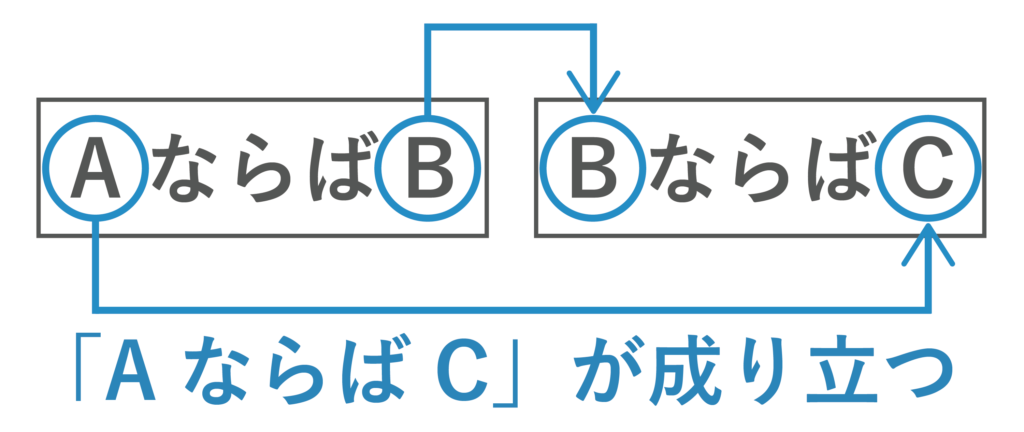
例えば「読書が好きならば勉強が好き」と「勉強が好きならば野球が好き」が成り立つとき、「読書が好きならば野球が好き」が成り立ちます。
三段論法自体はそこまで難しくはないでしょう。
【TG-WEB】三段論法と一緒に覚えておくべきこと
TG-WEBを受検予定の就活生や転職活動中の社会人は三段論法と一緒に命題の知識も必ず理解しておきましょう。
命題とは真偽を明確に判断できる文や式のことです。
命題には逆・裏・待遇という4つの概念があります。命題P「AならばB」に対して、
- 「BならばA」をPの逆
- 「AでないならばBでない」をPの裏
- 「BでないならばAでない」を対偶
といいます。
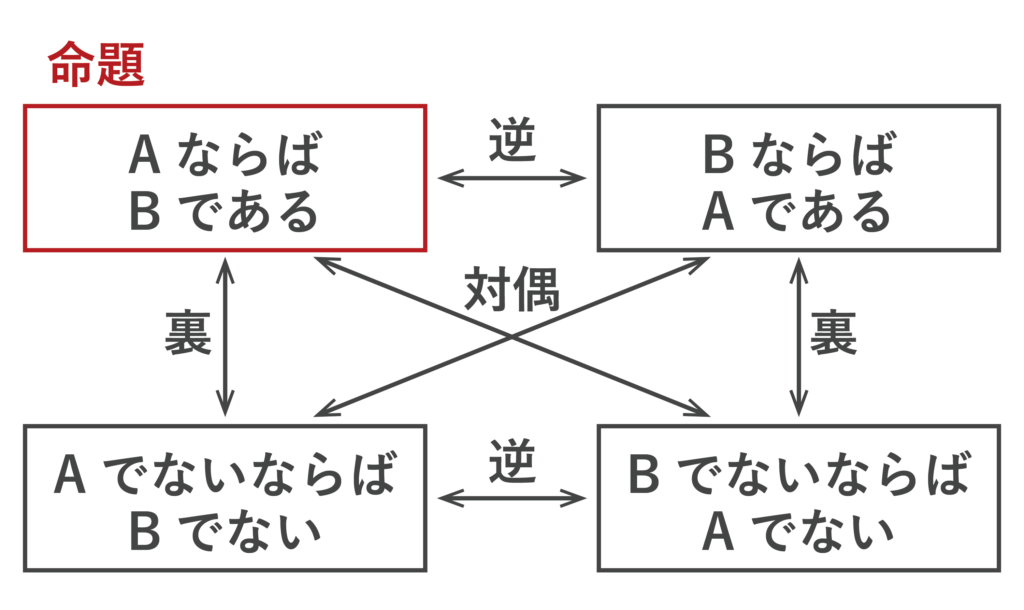
命題とその対偶の真偽は必ず一致します。
また、命題の裏は逆の対偶なので、逆と裏の真偽も必ず一致します。
例えば「Aが4の倍数ならばAは2の倍数である」という命題Pを考えてみましょう。
4=2×2なので、この命題は明らかに真(=正しい)であることがわかります。
よって、この命題Pの対偶「Aが2の倍数でないならばAは4の倍数でない」という新しい命題も真となります。
また、命題Pの逆は「Aが2の倍数ならばAは4の倍数である」です。
これはA=2のとき成り立たないので、偽となります。
よって、命題Pの裏である「Aが4の倍数でないならばAは2の倍数でない」も偽となります。
実際にこの命題の真偽を確かめてみると、A=2(4の倍数でない)のときAは2の倍数になっているので、偽であることがわかります。
TG-WEBの計数では命題と三段論法を組み合わせた問題が出題されるので、上記は必ず覚えておきましょう。
🔽 本にも載ってない極秘情報 🔽
【TG-WEB】三段論法の例題
三段論法と命題の逆・裏・対偶が理解できたところで、ここからは三段論法の例題を解いてみましょう。
制限時間=1分を目安に解いてみてください。
【例題】
「数学が好きな人は理科が好きである」「社会が好きな人は国語が好きである」「数学が好きでない人は国語が好きである」という3つの命題が成立するとき、確実にいえることはどれか。1つ選びなさい。
- 理科が好きな人は国語が好きでない
- 国語が好きな人は社会が好きで、数学が好きでない
- 国語が好きでない人は理科が好きである
【解答&解説】
好き=〇、好きでない=×で表現するとします。また「ならば」を「→」で表現するとします。
「数学〇→理科〇」の対偶は「理科×→数学×」です。
「社会〇→国語〇」の対偶は「国語×→社会×」です。
「数学×→国語〇」の対偶は「国語×→数学〇」です。
「国語×→数学〇」と「数学〇→理科〇」をつなげると「国語×→理科〇」となります。
よって、答えは3・・・(答)です。
TG-WEBでは三段論法と対偶を使うことで鎖のようにつながる限り、仮定をどんどん展開していくことが可能です。
【TG-WEB】三段論法の練習問題
最後に、三段論法の練習問題をご用意しました。
TG-WEBの計数で出題される問題の難易度に近いので、ぜひ解いてみてください。
【練習問題】
「笑顔の人は信頼される」「素直な人は笑顔の人である」「素直でない人は行動力がある」という3つの命題が成立するとき、正しいものの組み合わせは1〜5のうちどれか。
ア:素直な人は信頼される
イ:笑顔でない人は信頼されない
ウ:行動力のある人は信頼される
エ:笑顔でない人は行動力がある
- アとイ
- アとウ
- アとエ
- イとウ
- ウとエ
【解答&解説】
「笑顔〇→信頼〇」の対偶は「信頼×→笑顔×」です。
「素直〇→笑顔〇」の対偶は「笑顔×→素直×」です。
「素直×→行動〇」の対偶は「行動×→素直〇」です。
「素直〇→笑顔〇」と「笑顔〇→信頼〇」を三段論法でつなげると「素直〇→信頼〇」となります。
「笑顔×→素直×」と「素直×→行動〇」を三段論法でつなげると「笑顔×→行動〇」となります。
よって、正解は3・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
今回はTG-WEBの三段論法を取り上げました。
三段論法の意味自体は難しくありませんが、命題と組み合わせると混乱しやすくなります。
TG-WEBを受検予定の就活生や転職活動中の社会人は対偶と三段論法を上手く組み合わせることを意識しましょう。


