
TG-WEBでは集合に関する問題が出題されるのか?という疑問を持っている人もいますが、結論 出題されません(後ほど詳しく解説します)
※「TG-WEBとは?対策法や例題を完全解説!TG-WEBはこれで完璧だ」もぜひ参考にしてください。
本記事ではTG-WEBを今までに100回以上も受検してきたTG-WEBマスターの私タケルが、TG-WEBと集合の関係について解説した後、集合が出題されるWEBテスト(適性検査)をご紹介します。
ちなみにですが、TG-WEBにはたった3時間の勉強でTG-WEBが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものTG-WEB受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
TG-WEBで集合問題は出る?
本記事のタイトルと冒頭でも解説した通り、TG-WEBの計数で集合問題は出題されません。
TG-WEBには新型と従来型の2種類がありますが、それぞれの計数の出題範囲は以下の通りです。
- 新型=四則逆算、図表の読み取り
- 従来型=推論、図形、暗号、命題、数列など
※「TG-WEBの新型とは?旧型との見分け方は?出題される問題もご紹介」もぜひ合わせてご覧ください。
「集合」とは漢字の通り「集まり」のことです。
例えば、1〜5までの自然数の集合は1、2、3、4、5となります。
集合の問題例は以下です。
【例題】
ある学校の生徒60人のうち、通学に電車だけを利用しているのは40人、電車とバスの両方を利用している人は4人、どちらも利用していない人は5人だった。このとき、バスだけを利用している人は何人か。
【解答&解説】
与えられた条件をベン図にすると以下のようになります。
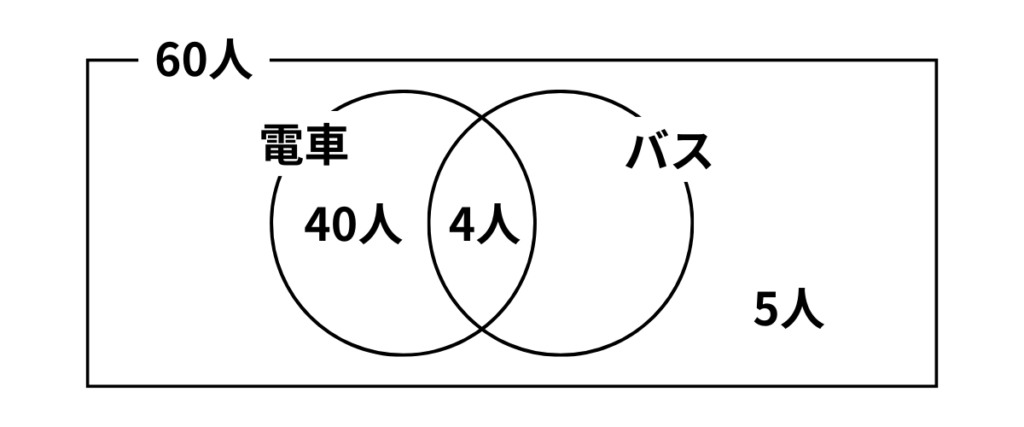
どちらも利用していない人が5人なので、どちらかを利用している人は60-5=55[人]です。
バスだけは「どちらか利用-電車だけ-両方」なので、55-40-4=11[人]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
集合問題が出るWEBテスト(適性検査)は?
TG-WEBの計数で集合問題が出ることはありませんが、SPIでは出題される可能性があります。
SPIは適性検査市場でシェアNo.1を占めており、導入社数は15,000社を超えています。
多くの就活生・転職活動中の社会人が受検しているWEBテストであり、かなり有名です。
※SPIの詳細については「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」をご覧ください。
SPIでは以下のような難易度の集合問題が出題されます。
【例題】
84人の子供のうち、算数が好きな子供は51人、国語が好きな子供は28人だった。どちらか一方だけ好きな子供が59人のとき、両方好きな子供は何人か。
【解答&解説】
与えられた条件をベン図にすると以下のようになります。
※両方好きな子供の人数=X人とします。

すると、算数だけ好きな子供の人数は(51-X)人となります。
また、国語だけ好きな子供の人数は(28-X)人となります。
どちらか一方だけ好きな子供の人数59人は(51-X)+(28-X)なので、(51-X)+(28-X)=59という方程式が立てられます。
これを整理すると、79-2X=59より、2X=20となるので、X=10[人]・・・(答)となります。
集合問題はカルノー表を使って解くことも可能
集合問題は上記でご紹介したようなベン図を使って解くことも可能すが、カルノー表を使って解くことも可能です。
カルノー表の例は以下です。
| お酒が好き | お酒が嫌い | 合計 | |
|---|---|---|---|
| 紅茶が好き | 32人 | 10人 | 42人 |
| 紅茶が嫌い | 12人 | 6人 | 28人 |
| 合計 | 44人 | 16人 | 60人 |
上記のカルノー表を使えば、
- 紅茶もお酒も好きな人=32人
- お酒が好きで紅茶が嫌いな人=12人
- お酒が嫌いで紅茶が好きな人=10人
- 紅茶もお酒も嫌いな人=16人
であることが視覚的にわかります。
カルノー表では縦の合計と横の合計が等しくなるのが特徴です。
上記のカルノー表の場合、縦の合計(44+16)と横の合計(42+28)はともに60で等しくなっています。
カルノー表を使うと以下のような集合問題をベン図を使わずに解けます。
【例題】
小学生180人を対象に実施したアンケートで、トンカツが好きな児童は112人、オムライスが好きな児童は69人であり、どちらも好きだと答えた児童がトンカツを好きだと答えた児童の3/8いた。どちらも好きでないと答えた児童は何人か求めよ。
【解答&解説】
以下のようなカルノー表を作成し、問題文から分かる箇所を埋めていきます。
| オムライスが好き | オムライスが好きでない | 合計 | |
|---|---|---|---|
| トンカツが好き | 112×3/8=42[人] | A人 | 112人 |
| トンカツが好きでない | B人 | C人 | D人 |
| 合計 | 69人 | E人 | 180人 |
すると、
- A=112-42=70
- B=69-42=27
- D=180-112=68
- C=D-B=68-27=41
- E=180-69=111
であることがわかります。
トンカツとオムライスどちらも好きでないと答えた児童はCなので、答えは41人・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はTG-WEBで集合問題は出るのかについて解説していきました。
集合問題はSPIで頻出なので、SPIを受検予定の就活生や転職活動中の社会人は必ず対策しておきましょう。


