
TG-WEBの旧型の計数では一筆書きに関する問題が出題されることがあります。
※「TG-WEBとは?対策法や例題を完全解説!TG-WEBはこれで完璧だ」もぜひ参考にしてください。
一筆書き問題は解き方のコツを知っていないと解くのが難しいので、必ずコツを理解しておきましょう。
本記事ではTG-WEBを今までに100回以上も受検しているTG-WEBマスターの私タケルが、一筆書き問題のコツを例題でわかりやすく解説していきます。
TG-WEBを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、TG-WEBにはたった3時間の勉強でTG-WEBが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものTG-WEB受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【TG-WEB】一筆書き問題の例題
一筆書きは道順や図形の対角線を一筆書きで進む問題です。
TG-WEBの計数の中でも特に難しい問題なので、TG-WEBで高得点を狙っている人は必ず対策しておきましょう。
※「TG-WEBは難しい・難しすぎるので要注意!3時間の勉強で通過する極秘裏ワザをご紹介」もぜひ参考にしてください。
まずはTG-WEBで出題される一筆書き問題のイメージを掴んでいただくために、例題を1問解いてみましょう。
【例題】
以下の図のような道とA〜Gの7つの建物がある。スタート地点から歩き出し、ある建物の前の道だけを通らずに、それ以外の道はすべて1回ずつ通って、ゴール地点に到着した。このとき、通らなかった道にある建物はどれか。A〜Gの中から1つ選びなさい。
・出典:『これが本当のWebテストだ!2』講談社
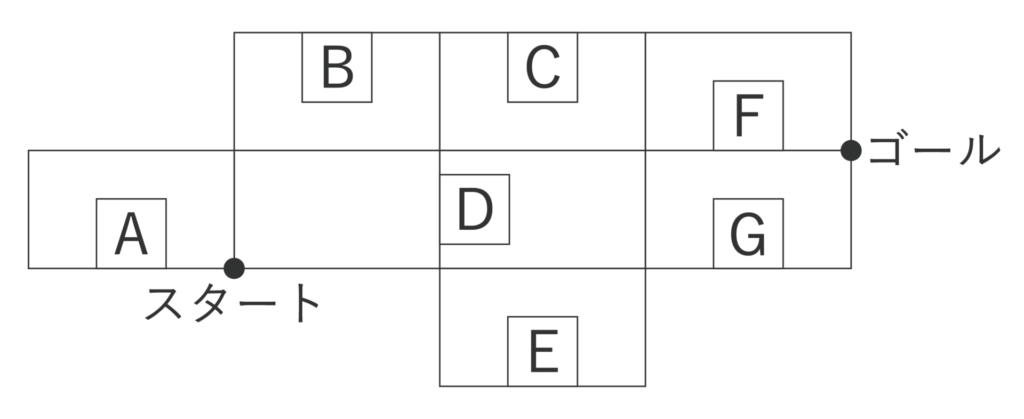
【解答&解説】
一筆書きができるのは「奇点が0個または2個」のときです。
以下の図のように道を線と考え、曲がり角や交差点などの「点」に線が何本集まっているかを数えたとき、点に集まる線が奇数本のときは「奇点」、偶数本のときは「偶点」と呼びます。
以下の図だと2と4は偶点、3は奇点になります。
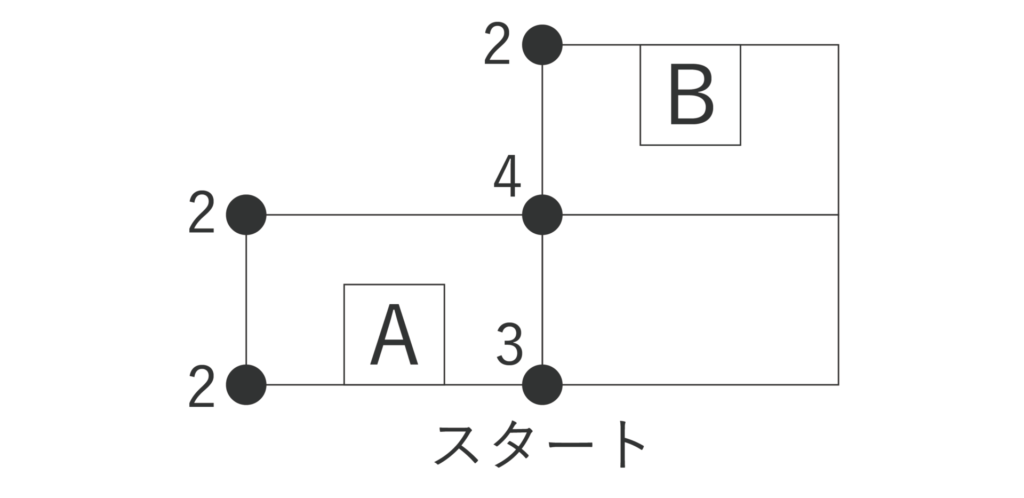
奇点が0個の場合、どの点からスタートしても、元の点に戻れます。
奇点が2個の場合、奇点からスタートして、もう1個の奇点がゴールとなります。
今回の問題ではスタートとゴールの位置が異なるので、一筆書きができるのは奇点が2個のときです。
まずはすべての点について、線が何本集まっているのかを以下のように記載していきます。
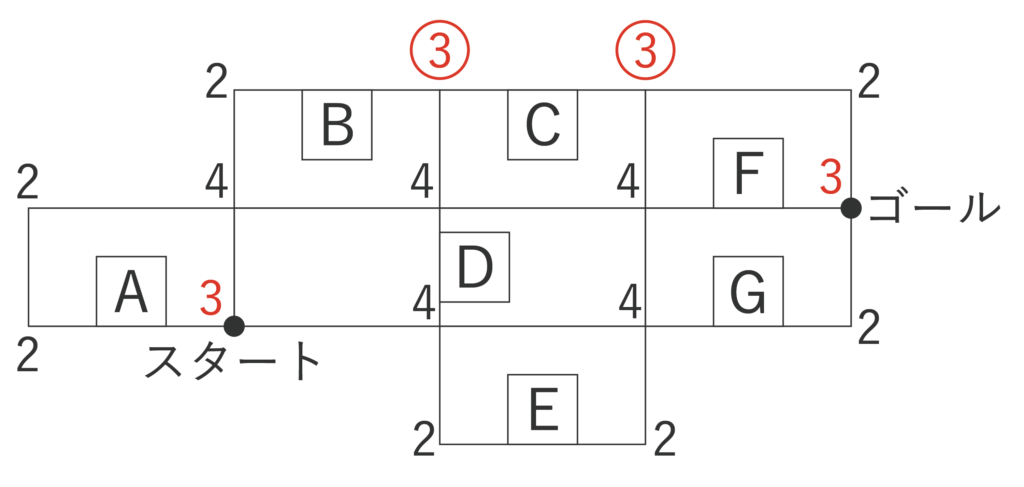
奇点は4個(いずれも赤字の3)です。このうち、赤丸で囲った2つの3が偶点になれば、奇点がスタートとゴールの2個となり、一筆書きできます。
この時点で、通らなかったのは建物C・・・(答)の前の道であることがわかります。
以下のように、建物Cの前を通らない場合は建物Cの左右が2になり、全体の奇点が2個になります。
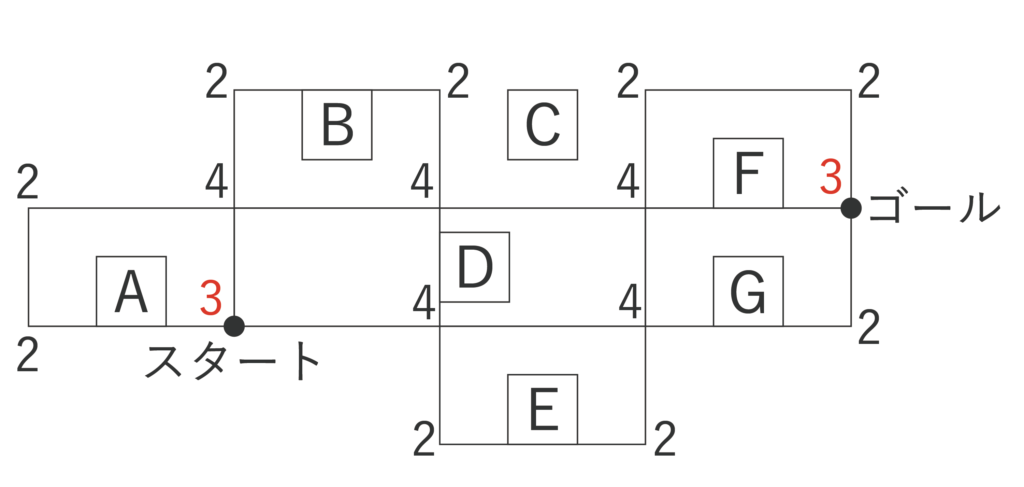
【TG-WEB】一筆書き問題のコツ
上記でご紹介した例題の通り、TG-WEBの一筆書き問題は「奇点が0個または2個のときのみ一筆書きが可能である」ということを知らないと絶対に解けません。
なので、TG-WEBを受検予定の就活生や転職活動中の社会人は上記は絶対に覚えておきましょう。
その上で、与えられた図に奇点と偶点を書き込んでいき、どうすれば奇点を0個または2個にできるか?を考えるのがポイントです。
🔽 本にも載ってない極秘情報 🔽
【TG-WEB】一筆書きの練習問題
最後に、一筆書きの練習問題を2問ご用意しました。
どちらもTG-WEBの計数で出題される問題の難易度に近いので、ぜひ解いてみてください。
【練習問題1】
図は正方形と正五角形に対角線を書き込んだものである。同様に、正六角形、正七角形、正八角形・・・正十二角形、正十三角形に対角線をすべて書き込んでいく。この10個の図形のうち、一筆書きできるものは全部でいくつあるか。
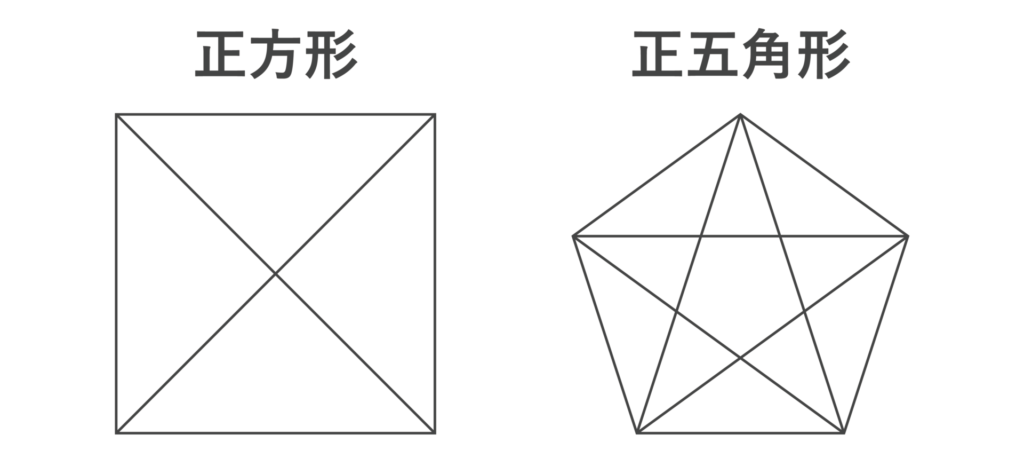
- 2個
- 3個
- 4個
- 5個
- 6個
【解答&解説】
繰り返しにはなりますが、一筆書きができるのは「奇点が0個または2個」のときのみです。
まず、正方形・正五角形・正六角形の場合を調べてみます。
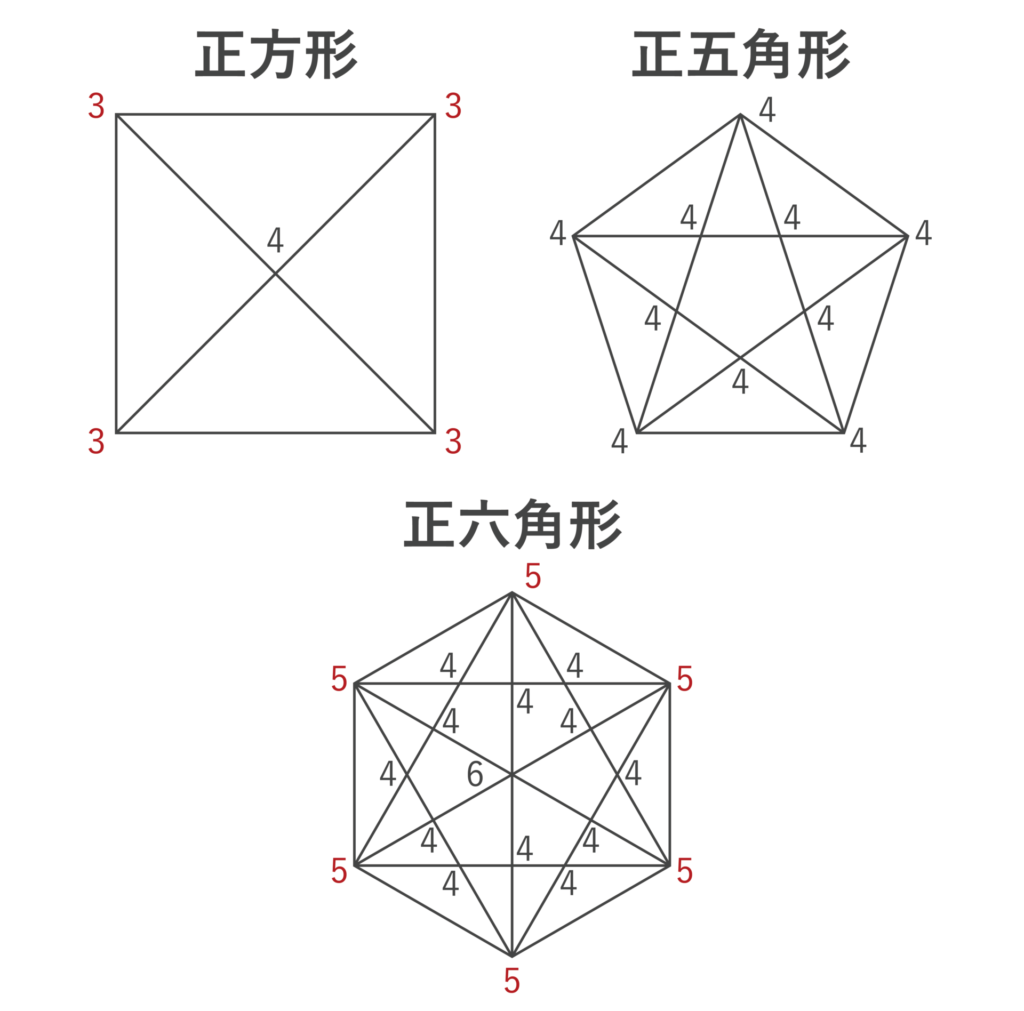
以上より、
- 正方形=奇点が4個なので、一筆書きできない
- 正五角形=奇点が0個なので、一筆書きできる
- 正六角形=奇点が6個なので、一筆書きできない
となります。
また、上記の図から、対角線同士の交点は必ず「偶点」になることがわかります。
各頂点に集まる線の数は「多角形の角数-1」なので、正方形は3、正五角形は4、正六角形は5・・・となります。
各頂点に集まる線の数が偶数(偶点)なら「奇点=0個」となり、一筆書きができます。
あてはまるのは多角形の角数=奇数のときなので、正五角形・正七角形・正九角形・正十一角形・正十三角形の5つです。
よって、正解は4・・・(答)です。
【練習問題2】
次の図形のうち、一筆書きができるものはどれか。1つ選びなさい。
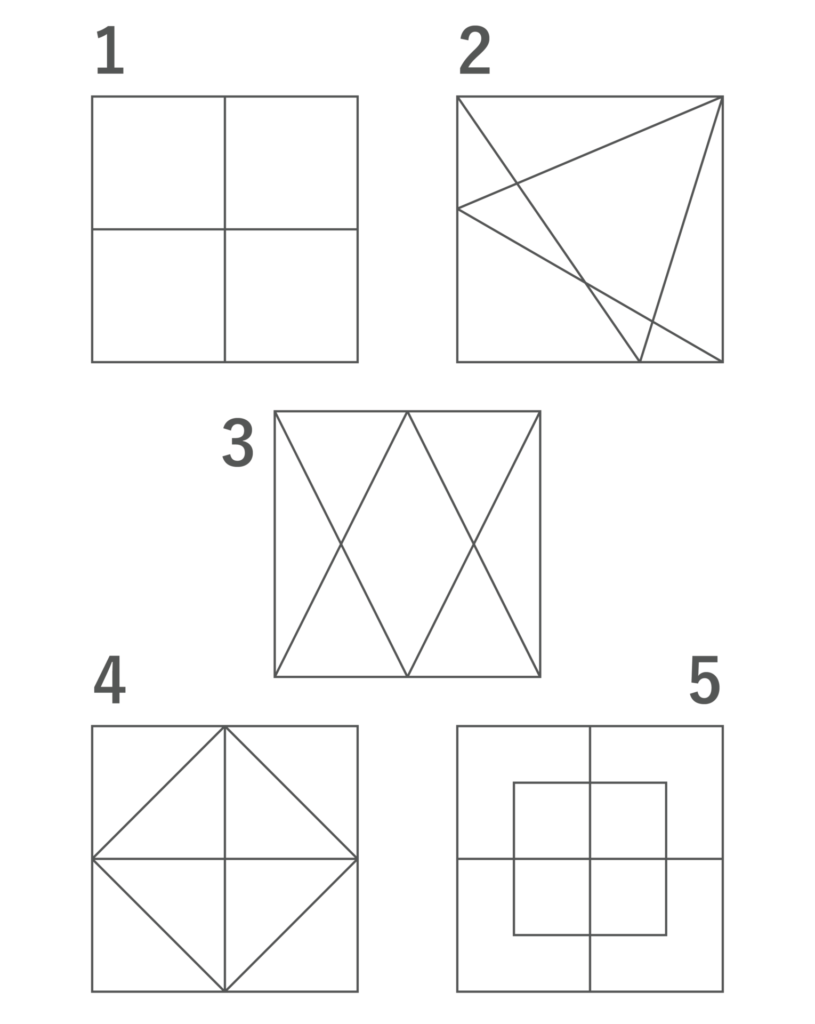
【解答&解説】
選択肢それぞれの図形の各頂点に集まる線の本数を記入すると、以下の図のようになり、奇点(図の色の付いた点)の数を数えると、選択肢2は2個で、それ以外は4個であることがわかります。
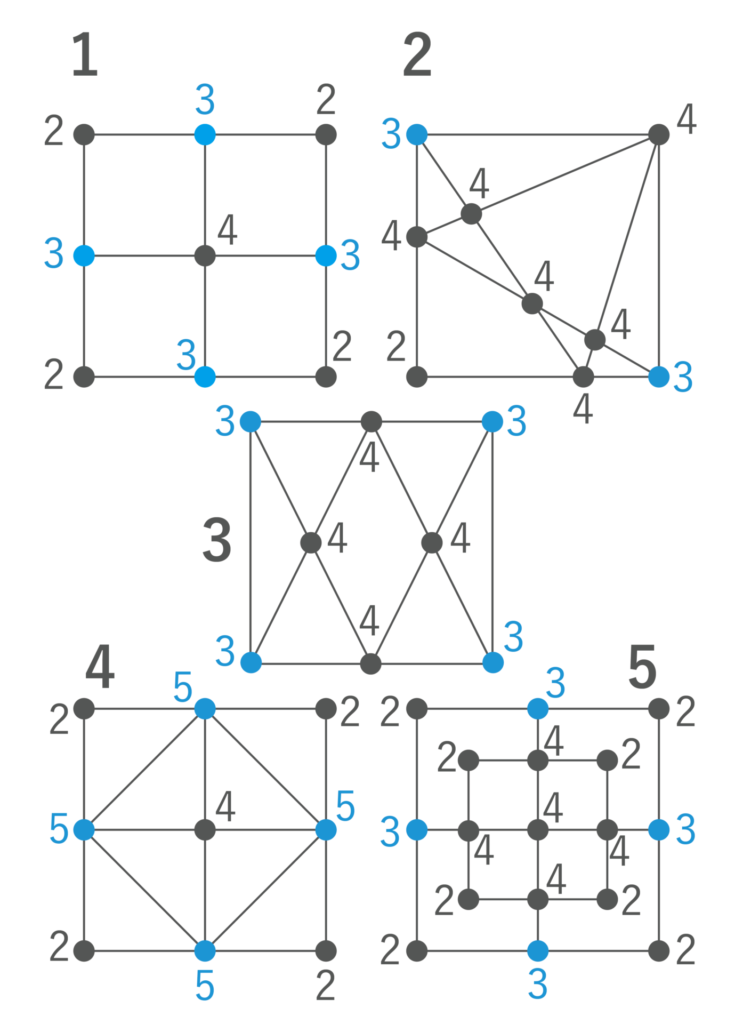
以上より、正解は2・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はTG-WEBの計数で出題される一筆書き問題を取り上げました。
本記事で奇点・偶点という言葉を初めて聞いた人もいるかと思います。TG-WEBを受検予定の人は必ず理解しておきましょう。


